Yes, Newton’s three laws are all based on mathematical formulas, but the equations would be too complex for this text. They are defined (some with applicable mathematical notation) as follows: Newton’s First Law (Law of Inertia) states that without any forces acting on an object, it will maintain a constant velocity. In other words, an object will stay still or keep moving in a straight line until something pushes it to change its speed or direction. The one force that stops almost everything from standing completely still or moving in a straight line is gravity. This is easily seen when you throw a baseball in the air: The ball does not move in one, continuous, straight direction because the Earth’s gravity pulls it downward toward the surface.

Newton’s Second Law (Law of Constant Acceleration) states that if a force acts on an object, the object accelerates in the direction of the force; the force creates an acceleration proportional to the force (and inversely proportional to the mass). This is written in the following notation: F = ma, in which F is the force, m is the mass, and a is the acceleration. Newton actually expressed this in terms of the calculus—a form of mathematics he created to explain these physical laws (for more about the calculus and Newton, see “History of Mathematics” and “Mathematical Analysis”). He wrote the equation as follows:

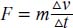
in which m is mass, Δv is the change in velocity, and Δt is the change in time. This is because instantaneous acceleration is equal to the instantaneous change in velocity in an instance in time (or change in time).

Newton’s Third Law (or Law of Conservation of Momentum) states that forces on an object are always mutual. To put it another way, if a force is exerted on an object, the object reacts with an equal and opposite force on the phenomenon that initially exerted the force. Simply stated, objects exert equal but opposite forces on each other. This is often phrased, “For every action, there is an equal and opposite reaction.” The mathematical equations for these forces are complex and beyond the scope of this text.