Geometry and TrigonometryBasics of Geometry |
How are angles measured? |
Angles are measured in two major ways: degrees and radians. Similar to degrees on a temperature scale, degrees in mathematics—especially when discussing angles—are usually denoted by the symbol °; they are divided into 60 arc minutes, and arc minutes are divided into 60 arc seconds. The multiples of 60 are thought to be connected to the Babylonian’s sexagesimal number system (one based on the number 60), in which the year was composed of 360 days (or 12 months at 30 days each). If the vertex of an angle and one side are fixed and the other side is rotated about the vertex, it sweeps out a circle of 360° with each complete rotation. Said another way, a full rotation is 360 degrees.
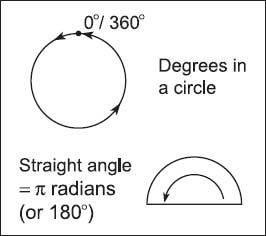
The angles of a circle are typically measured either in degrees or radians (rad). There are 360 degrees in a circle, or 2π × 1 rad.
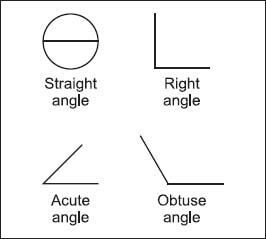
The four basic types of angles are straight, acute, obtuse, and right.
Radians (denoted as rad) are real numbers represented as an angle; they are the central angle of a circle determined by two radii and an arc joining them. In degrees, a radian is about 57.29578 degrees or 180/π degrees, because a semicircle contains π radians. For example, π/6 is equal to a 30 degree angle; because a straight angle is π radians (or 180°), if you divide 180 by 6, (or π/6), it is equal to 30 degrees. Radians are most often used in probability and statistics, or calculus, especially to obtain the derivative of trigonometric functions.
