When measuring the number of degrees in a circle, another unit called radians is often used in trigonometry. It is known that a circle is 360 degrees, with 1 degree equal to 60 minutes (60’) and 1 minute equal to 60 seconds (60’); this is also called DMS (Degree-Minute-Second) notation. One revolution around the circle also measures 2π radians. Thus, 360° = 2π radians; or 180° = π radians. Simply put, to convert radians to degrees, multiply by 180/π; to convert degrees to radians, multiply by π/180. The following are examples of how to convert degrees and radians:

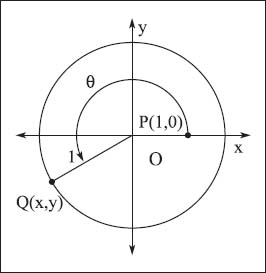
In this example of an angle measured using trigonometry, x² + y² = 1.

Convert the angle 236.345° to DMS notation (by breaking down the decimals into minutes and seconds):

236° + 0.345° × 60’ /1°

236° + 20.7’ = 236° + 20’ + 0.7’ × 60’ /1’

= 236° 20’ 42”

Convert the angle 236.345° to radians (convert the entire amount into radians by multiplying π radians by 180°, which is actually equal to “1” since, from above, 180° = π radians):

236.345° × π radians/180° = (236.345 × 3.141592) radians/180°

= 4.124998 radians

And, conversely, convert 4.124998 radians to degrees:

4.124998 radians × 180°/3.141592

= 236.345°