Geometry plays an important part in the study of minerals. This is because certain minerals exhibit specific shapes called crystals, with specific crystalline forms occurring when a mineral’s atoms join in a particular pattern or internal structure. This arrangement is determined by several factors, including the chemistry and structure of the mineral’s atoms, or even the environment in which the crystal grew.

Overall, there are specific angles between corresponding faces of all crystals. Mineralogists (scientists who study minerals) divide these crystalline forms into 32 geometric classes of symmetry; they use this information to identify and classify certain minerals.

The crystals are also subdivided into seven systems on the basis of an imaginary straight line that passes through a crystal’s center (or axis). The seven groups include cubic (or isometric), tetragonal, ortho-rhombic, monoclinic, triclinic, hexagonal, and trigonal (or rhombohedral). For example, a crystal in the cubic system has three axes that intersect at right angles; the axes are also of equal lengths. The best way to envision this crystal is to think of a box with equal sides—or a cube.

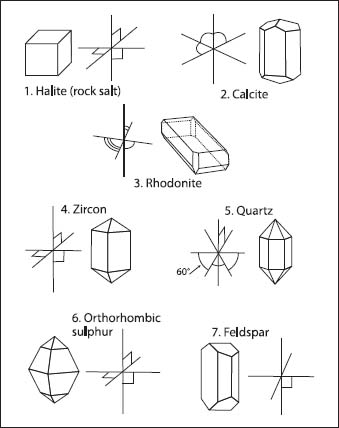
1. Halite is an example of a cubic (or isometric) system in which three equal axes are all at right angles. 2. Calcite is formed with a trigonal (or hombohedral) crystal system in which the three axes are set obliquely at equal angles to each other. 3. Rhodonite is a crystal formed by a triclinic system in which the three axes are unequal and set obliquely at unequal angles. 4. In a tetragonal system minerals such as zircon are formed by crystals with three axes, all at right angles, in which one axis is longer than the other two. 5. Quartz is an example of a hexagonal system in which three axes at 60° angles to each other are positioned around a vertical axis that can be longer or shorter than the other three. 6. In an orthorhombic system (such as orthorhombic sulfur) the three axes are of unequal length and set at right angles to each other. 7. Finally, with a monoclinic system, two of three axes are at right angles with the third set obliquely, such as in the example of feldspar.