The length of this vector is 5.0 (see above to determine how to solve for length of the vector); or |V| = 5.0. Thus, the value of the normalized vector is given by:

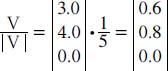
In this case, 0.6 squared equals 0.36; 0.8 squared equals 0.64. Both added together with the zero equals 1. (If the vector is already normalized, then the value of |V| will be equal to one, and after division the vector will remain as it was before.)

Vectors can be found in two-, three-, or multi-dimensional space. Two-dimensional vectors are seen visually on a graph as a line with an arrow connecting two points. A two dimensional vector is defined by length and direction measured by the angles that the arrow makes with the x and y coordinate system axes; a vector in such a coordinate system is written as two components, (x, y).

Vectors in a three-dimensional space are represented with three numbers, one along each coordinate axis. These are the coordinates of the arrow point, usually as (x, y, z) if the arrow starts at the origin. A more complex vector is one with multiple components, in which several different numbers in ordered n-tuples represent a vector. For example, (4, 1, -2, 0) is an ordered 4-tuple representing a vector in four dimensions.