Math in EngineeringIndustrial Andaeronautical Engineering |
How do engineers determine the escape velocity of a rocket? |
A ball thrown into the air will rise and then return, thanks to the Earth’s gravity. If the ball is given a larger initial velocity, it will rise even higher and then return. With even more velocity, the ball will reach a certain escape velocity, in which the ball “escapes” the gravitational pull of the planet. If the ball is launched with an initial velocity greater than the escape velocity, it will rise and not return. In this case, physicists say that the ball was given enough kinetic energy to overcome all of the negative gravitational potential energy—or, it launches into space. Thus, if m is the mass of the ball, M is the mass of the Earth, G is the gravitational constant, v is the velocity, and R is the radius of the Earth, then the potential energy is equal to GmM/R. The kinetic energy of the launched ball is equal to mv2/2. That means the escape velocity is equal to:
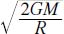
This is independent of the mass of the ball. To see how this works to an aerospace engineer, just replace the word “ball” with “space vehicle.”
