Mathematical AnalysisCalculus Basics |
How is infinity treated when discussing limits? |
Defining infinity is a definite part of calculus, especially when discussing limits and “negative” and “positive” infinity. Whenever the inverse of a small number is taken, a large number is generated, and vice versa. In calculus, this is written as:
But ±∞ are no ordinary numbers, because they do not obey the usual rules of arithmetic, such as ∞ + 1 = ∞; ∞ - 1 = ∞; 2 × ∞ = ∞; and so on. Therefore, in calculus functions, and thus limits, infinity is treated much differently. For example, for the function f(x) = 1/x - 3, when x → 3, then x - 3 → 0. The limit function then becomes:
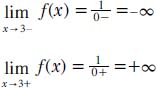
This example can be seen in the accompanying graph.
