Geometry and TrigonometryMeasurements and Transformations |
How is the area determined for some common two-dimensional polygons? |
Finding the areas of polygons is not as simple as determining the areas of a rectangle and square. In order to find the area of certain polygons, one essentially “breaks the shape down” into smaller shapes with simpler formulas; these types of shapes are called composites. The formulas for many of these polygons are all adaptations from the rectangle area formula—or height (h) times base (b). For example, a triangle is actually exactly half of a rectangle. Thus, the formula to find the area of a triangle is half the base times the height (1/2bh). In the case of the trapezoid, the figure can be divided into triangular sections, with the area equal to one half times the two bases times the height, or ½(B + b)h.
The triangle formula also is used to find other regular polygon areas, but they are less obvious. For a regular polygon, a feature called the apothem is necessary for finding the area. This is the height of one of the congruent triangles inside the regular polygon. In general, to find the polygon’s area, you need to find the area of one triangle and multiply it times the number of sides. For example, to find the area of a hexagon, divide the figure into six triangles, each with l equal to the height of each interior triangle or apothem; l is also half of the smallest interior dimension of the hexagon, called w. Thus, the area of a hexagon is the square root of 3 divided by 2 times w squared (or 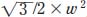 ).
).
There is still another way to determine the area of a polygon by using the Pythagorean theorem, a method that uses length and height, with the resulting formula for the area of a polygon looking much different. Both methods give the same results in numerical terms. For example, the area of a hexagon using the smallest interior dimension would be 0.866 times the square of the smallest width, w; the area of a regular hexagon using the Pythagorean theorem is 2.598 times the square of its side length. These may be different ways of presenting the solution, but both give the same correct area measurements.
