Geometry and TrigonometryMeasurements and Transformations |
How was the area of a circle first determined? |
When it comes to determining the area of a circle, there are many historical claims to this solution. One of the earliest techniques may have been the Chinese “comb” method, in which a circle is cut into n wedges, each 360/n degrees and each piece identical (with the same area). To see how this works, take the bottom half of a unit circle and cut it into wedges like slices of a pie; place all the wedges next to each other, with the points up (like the teeth of a comb or animal). Then split the top half of the circle in the same way, putting them next to each other above the other wedges, but this time point the tips of the wedges down. Close the “teeth”; as n goes to infinity, the shape of the combined wedges approaches a rectangle. Taking the formula for determining the area of a rectangle (width times height), the width is πr (or half the circumference) and the height is r. Thus, the area is πr2.
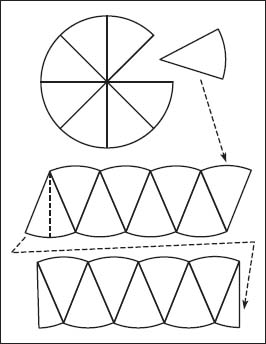
To calculate the area of a circle, the Chinese devised the Chinese comb method in which a circle is divided into pie slices and rearranged into a rectangle to greatly simplify the math involved.
