A tool called Napier’s Bones (also called Napier’s Rods) was invented by Scottish mathematician John Napier (1550–1617). These were multiplication tables inscribed on strips (also called rods) of bone (not Napier’s, but animal bone), ivory, or wood. He published the idea in his book Rabdologia, which contained a description of the rods that aided in multiplication, division, and the extraction of square roots. (For more about Napier, see “Algebra.”)

Each bone is a multiplication table for a single digit, with the digit appearing at the top of its bone. As seen below, consecutive, non-zero products of this digit are carved in the rod, with each product occupying a single cell. For example, to multiply 63 by 6, the two bones or rods corresponding to 6 and 3 would be put alongside each other and would look like the following illustration.

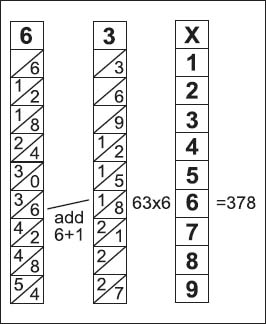
In this example of how to use Napier’s Bones, 63 is multiplied by 6 to get the correct result of 378.

The first number would be the number in the diagonal at the sixth position (3); then the product (or solution) is evaluated diagonally, or by adding the two numbers diagonal from each other, or 7 (6 + 1); and the next number in the separate diagonal, or 8. In other words, 63 × 6 = 378.

Initially, the tables were used by merchants to speed up calculations. German astronomer and mathematician Wilhelm Schickard (1592–1635) would eventually build the first calculating machine based on Napier’s Bones in 1623. His device could add, subtract, and, with help, multiply or divide. This is why he is often called the “father of the computing era” (see below).