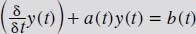Mathematical AnalysisDifferential Equations |
What are first-order homogeneous and non-homogeneous linear differential equations? |
These differential equations may be long-winded phrases, but they are actually types of first-order differential equations. A first-order homogeneous linear differential equation can be written in the notation as follows:
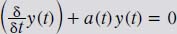
The first-order homogeneous linear differential equations are those that place all terms that include the unknown equation and its derivative on the left-hand side of the equation; on the right-hand side, it is set equal to zero for all t.
The non-homogeneous linear differential equations are those that, after isolating the linear terms containing y(t) and the partial differentials inside the above large parentheses on the left side of the equation, do not set the right-hand side identically to zero. It is often represented by one function, such as the b(t) (see below). The standard notation is as follows: