There are numerous terms used in the Cartesian coordinate system. Besides the ones already mentioned, the following are some of the most common.

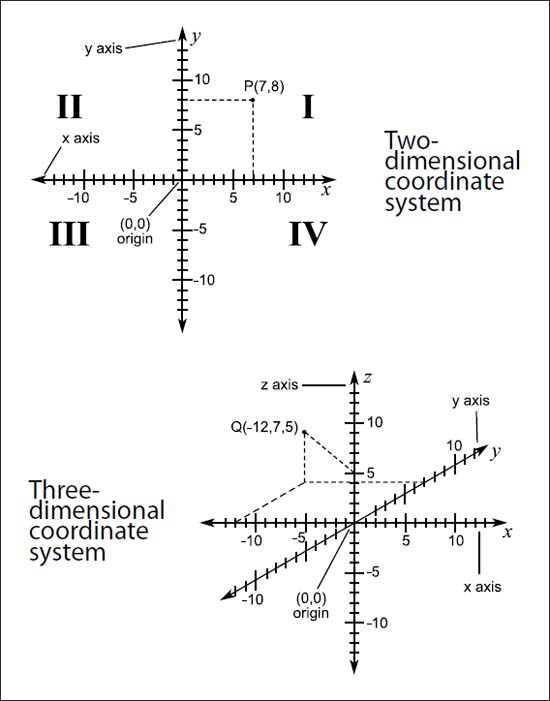
The four quadrants of a two-dimensional coordinate system are indicated above by the Roman numerals I, II, III, and IV. A three-dimensional coordinate system (bottom) adds a z axis so points can be indicated in real space, such as with point Q(-12, 7, 5) in this illustration.

An intercept is a point’s distance on a coordinate system axis from the origin to where a curve or surface intersects the axis. On a graph, the x-intercept and y-intercept are two important features that show where a line cuts through the x and y axes, respectively. The origin is the fixed point from which measurements are taken. In most cases—especially in a standard, simple two-dimensional Cartesian coordinate system—this means the point that represents zero. This is often seen as (0, 0), or the point in which the x and y axes intersect on a graph. In a three-dimensional system, the coordinates are often seen as (0, 0, 0).

A Cartesian plane (or coordinate plane) is described as a two-dimensional space made up of points that are identified by their relation to the origin (zero), and the x and y axes. An axis (the plural is axes) is a reference line used in a graph or a coordinate system, such as the Cartesian system. For example, the x-axis and y-axis are perpendicular lines on a graph in a two-dimensional system; in a three-dimensional system, they are the x-axis, y-axis, and z-axis.

Collinear points are those that lie on a straight line. Any two points are considered collinear because a straight line passes through both. Many procedures in analytic geometry involve determining the collinear points that represent coordinates that solve an equation. Logically, those points that do not lie on the same line—or, in other words, that do not solve the equation—are called non-collinear points.