Recreational MathMathematical Games |
What are the odds of winning the powerball lottery? |
It was eventually going to happen: A number of lottery-offering states got together to have lotteries with huge amounts of prize money. The resulting powerball lotteries have been very lucrative—not for the players, but for the states. Such gigantic sums of money tempt quite a few people to take the risk, with many buying hundreds of tickets in an attempt to better their odds.
But does it work? Not really. There is a way to determine the odds of such “lotto-type” lotteries in which numbered balls (or numbers) are randomly chosen to represent a winning number. This is usually expressed as: n! / (n - r)! r!, in which n is the highest numbered ball and r is the number of balls chosen. (The n! is “n-factorial”; for more information about factorials, see “Algebra.”)
In math, this type of equation is called a combination. For example, if there are 50 balls and 5 are chosen, there are 50 possible numbers that can come up first, leaving 49 that can come up second, and so on. The equation becomes:
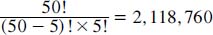
or the chances of winning are about 2 million to 1.
