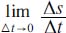There are two major ways of looking at the derivative—the geometrical (or the slope of a curve) and the physical (the rate of change). The derivative was historically developed from finding the tangent line to a curve at a point (geometrically); it eventually became the study of the limit of a quotient usually seen as the change in x and y (Δy/Δx). Even today, mathematicians debate which is the best way to describe a derivative.

Geometrically, after determining the slope of a straight line through two points on a graph of a function, and the limit where the change in x approaches zero, the ratio becomes the derivative dy/dx. This represents the slope of a line that touches the curve at a single point—or the tangent line.

Physically, the derivative of y with respect to x describes the rate of change in y for a change in x. The independent variable, in this case x, is often expressed as time. For example, velocity is often expressed in terms of s, the distance traveled, and t, the elapsed time. In terms of average velocity, it can be expressed as Δs/Δt. But for instantaneous velocity, or as Δt gets smaller and smaller, we need to use limits—or the instantaneous velocity at a point B is equal to: