Triangles (or “three angles”) are polygons with three sides. A triangle’s three line segments (or sides) are joined together at three vertices (endpoints). For all triangles, the sum of a triangle’s three interior angles is equal to a straight angle, or 180 degrees.

Triangles are classified by either the lengths of their sides, or, more commonly, the measurement of their angles. All triangles have at least two acute angles, but the third angle, which can be used to classify the triangle, can be acute, right, or obtuse (for more about these angles, see above). The types of triangles based on angles are:

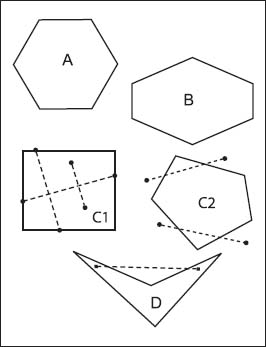
Types of polygons include regular hexagons (A), irregular hexagons (B), convex polygons (C1 and C2), and concave polygons (D).

Right triangle—There is one angle of 90 degrees.

Acute triangle—All three angles are less than 90 degrees, or the triangle has three acute angles.

Obtuse triangle—There is one angle greater than 90 degrees, or the triangle has one obtuse angle.

Equiangular triangle—An acute triangle in which all angles are congruent, or when all three angles are equal.

Triangles can be further classified by their sides, as in the following:

Scalene triangle—There are no sides—and therefore no angles—that are equal; in other words, no sides are congruent.

Isosceles triangle—Two of the sides are equal (congruent), and thus the base angles are equal.

Equilateral triangle—When all three sides are equal (congruent).