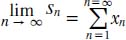Convergence of a series is related to the convergence of a sequence, but don’t confuse them. The convergence of the sequence of partial sums (usually written as {s_n}) differs greatly from the convergence of a sequence of numbers (usually written as {x_n}). For example, the series Σx_n (and its associated sequence of partial sums, or {s_n}), is convergent if and only if the sequence {s_n} is convergent. Thus, the total sum of the series is the limit of the sequence {s_n}, seen as: