Geometry and TrigonometryBasics of Geometry |
What does the term bisect mean? |
The term “bisect” is important in geometry; it means to cut into two (or divide into half), mainly lines (or two-dimensional figures) and angles. To compare, a bisected line segment means finding the plane, line, or point that is the midpoint of the line segment. This is also called a segment bisector. An angle bisector is a ray in the interior of an angle that forms two equal angles. First locate the point on each ray that is equally distant from the vertex; then draw a third point equally distant from each of the first two rays. A line that extends through the third point and the vertex is the angle bisector.
To draw a bisector, follow the following sequence (as per the illustration): First, draw an angle; then draw an arc centered at the vertex (endpoint), in which B and C are the intersections of the arc and angle lines at equal distances from the vertex; next draw an arc centered at B and one centered at C—both with the same radii—inside the angle; finally, extend a line from the vertex to the point D where the arcs of B and C intersect—making AD the bisector of the angle at A.
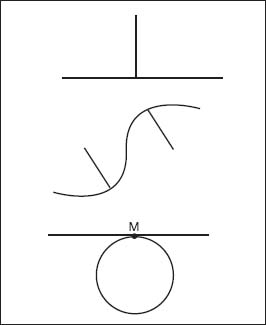
Examples of a perpendicular line (top), normal lines (middle), and tangential lines (bottom), with point M being the point of tangency.
