Foundations of MathematicsSet Theory |
What is Russell’s Paradox? |
Russell’s Paradox is one of the most famous of the set theory paradoxes. It first appears when studying the naive set theory: In this case, R is the set of all sets that are not members of themselves; from there, R is neither a member of itself nor a member of itself. The paradox sets in when you try to reason how a set appears to be a member of itself if and only if it is not a member of itself. Symbolically, it is expressed as follows:
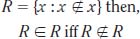
Discovered by Welsh mathematician and logician Bertrand Arthur William Russell (1872–1970) in 1901, the paradox sparked a great deal of work (and controversy) in logic, set theory, and especially in philosophy and foundations of mathematics. The reason why it became so important was its affect on mathematics: It created problems for those who based mathematics on logic, and it also indicated that something was wrong with Georg Cantor’s intuitive set theory. (For more about Russell and the paradox, see “History of Mathematics.”)
