A normalized (or unit) vector is one in which the sum of the squares of all coordinates is equal to one. For example, the vector (2, 2, 0) is not normalized; the vectors (0.707, 0.707, 0.0) and (1.0, 0.0, 0.0) are normalized. (An outward normal is another name for a normalized vector; it represents the direction that a polygon surface or vertex [end-point] is facing.) Normalized (or unit) vectors are often seen written as 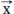, but more usually as 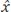(the is often referred to as a “hat”).

A vector can be normalized by calculating the magnitude or length of the vector and dividing each coordinate by this value. For example, consider the following vector: