Geometry and TrigonometryAnalytic Geometry |
What is an asymptotic curve? |
On a graph, a line that approaches close to a curve (or even an axis) but never quite reaches it is an asymptotic curve. In an example similar to one of Zeno’s paradoxes (see “Foundations of Mathematics”), if a kitten standing a yard from a box walks half the distance to the box each hour, it will technically never reach the box, because the distance it travels each hour is never more than half the remaining distance to the box. If this problem was illustrated as an equation, the answer would never quite reach its solution. A more mathematical example is the exponential function y = 2x, which results in a line that approaches but will never quite reach the x-axis.
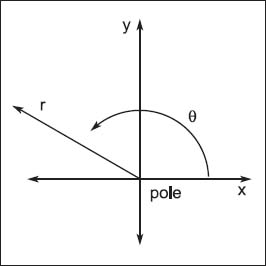
In the above illustration, × = r cos θ; y = r sin θ r2 = x2 + y2; and θ = arctan y/x (x=0).
