Geometry and TrigonometryTrigonometry |
What is an example of finding a trig function? |
One example of finding a trig function—including an illustration—follows: Find the trig functions of the angle θ = 60°. In this case, make a circle with a string extending two units; then measure 60° from the vertex (O). Drop a line perpendicular from the point on the circle to the initial line, creating a 90° angle; that makes the last angle 30°. Because the result is a right triangle, with the values of the hypotenuse (2) and the adjacent leg (1), the Pythagorean theorem (see elsewhere in this chapter) is used to determine the length of the other leg, or a2 + b2 = c2:
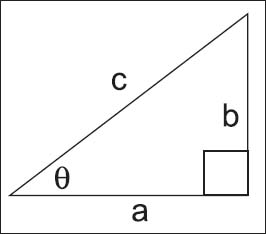
Trigonometric functions can be used to describe a right triangle.
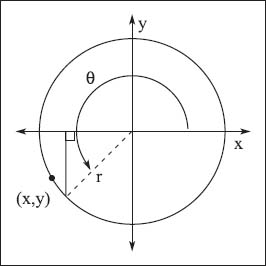
Trigonometric functions of a circle.
Thus, by figuring out the cos (adjacent/hypotenuse) and sin (opposite/hypotenuse) for the angle 60°, Q is at point 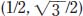 on the circle. The other trig functions can be determined using the methods in the questions above:
on the circle. The other trig functions can be determined using the methods in the questions above:
