Mathematical AnalysisDifferential Calculus |
What is the Mean-Value Theorem? |
The Mean-Value Theorem has nothing to do with crankiness, but it is one of the most important theoretical tools in the calculus. In written terms, it is defined as the following: If f (x) is defined and continuous on the interval [a, b], and differentiable on (a, b), then there is at least one number on the interval (a, b)—or a < c=""><>—such that:
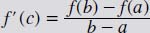
When f(a) = f(b), this is a special case called Rolle’s Theorem, when we know that f (c) will equal zero. Interpreting this, we know that there is a point on (a, b) that has a horizontal tangent.
It is also true that the Mean-Value Theorem can be put in terms of slopes. Thus, the last part of the above equation (on the right of the equal sign) represents the slope of a line passing through (a, f(a)) and (b, f(b)). Thus, this theory states that there is a point c ∈ (a, b), such that the tangent line is parallel to a line passing through the two points.
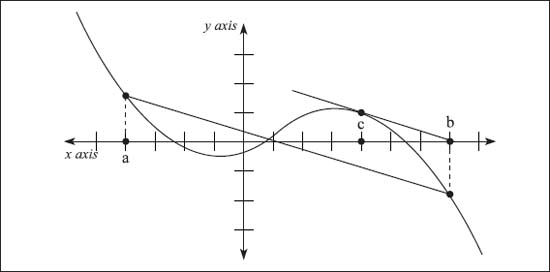
This graph illustrates the concept of the Mean-Value Theorem.
