The average deviation is a way of characterizing the spread (dispersion) among the measures in a given population. To determine the average deviation, compute the mean, then specify the distance between each score and that mean without regard to whether the score is above or below the mean. The following is the notation for this calculation (the symbol Σ stands for “sum of”; the symbol || stands for absolute value):

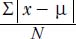
in which x is the various values of the samples, μ is the mean (or average) for the entire population, and N is the number of samples (the two vertical lines representing the absolute value means there are no negative numbers on top).

For example, if we have six people who weighed 166, 134, 189, 141, 178, and 150, the equation would read (μ is the average, or the total weight divided by the number of people, or 958/6 = 159.67; n = 6, or the number of people; and x are the individual weights of the people):

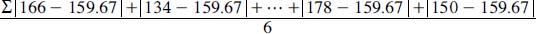
The average deviation for this example is 18.

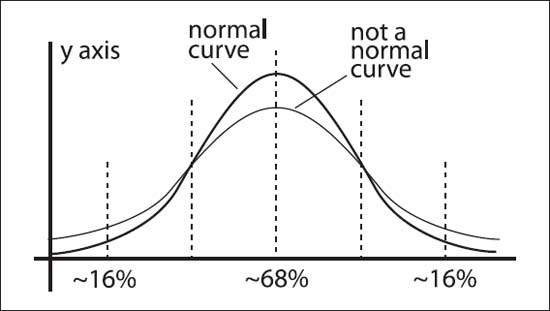
A “normal” curve has a bell shape to it into which the majority of a sampling of statistics falls within a certain average range.