Geometry and TrigonometryAnalytic Geometry |
What is the definition of a conic section? |
This family of curves—first discovered (as far as we know) by the ancient Greeks—is generated by planes intersecting (“cutting into”) a cone. The resulting feature depends on the angle between the plane and the axis of the cone, with none of the planes passing through the endpoint (vertex) of the cone. Each plane that cuts a cone creates a two dimensional figure called a section, thus the resulting figures are called conic sections or conics. In general, the possible resulting surfaces are a sphere (the cut perpendicular to the axis), ellipse (or the circle as a special case; a cut moderately inclined to the axis), parabola (a cut parallel to one of the straight lines that generate the cone), and hyperbola (using two cones tip to tip, the cut even more steeply inclined than all the others).
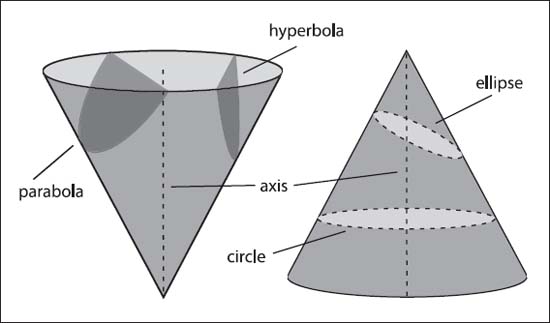
Depending on the way a plane intersects a cone shape, different types of curves will be the result.
