Math BasicsMore About Numbers |
What is the story behind the Mersenne primes? |
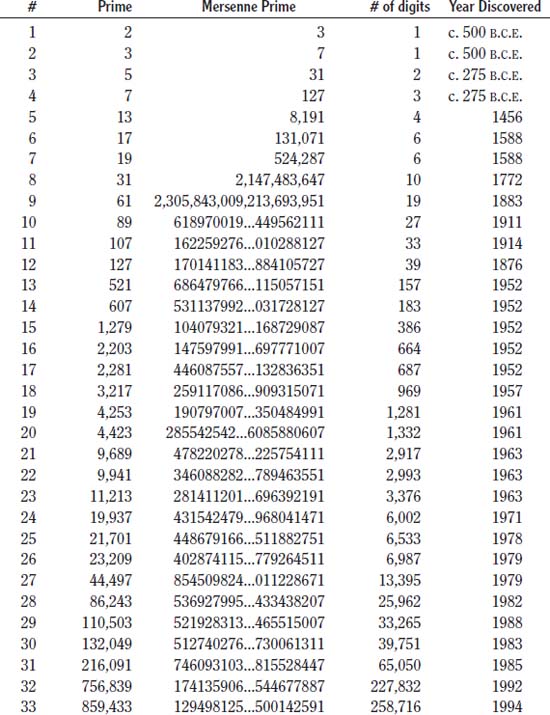
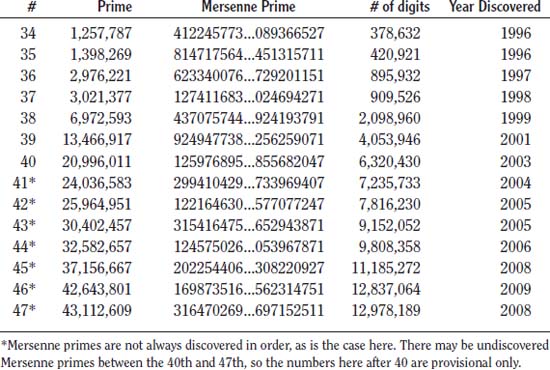
Mersenne primes (or Mersenne numbers) are connected to prime numbers. They are from the form 2p - 1, in which p is a prime; or said another way, when 2p - 1 is prime, it is said to be a Mersenne prime.
Centuries ago, many mathematicians believed that numbers from the form 2p - 1 (they actually used the form 2n - 1, which is the same as the 2p - 1 used today) were prime for all primes p. By the 16th century, it was proven that 211 - 1 = 2,047 was not prime. By 1603, Pietro Cataldi (1548–1626) correctly discovered that p = 17 and p = 19 were both prime, but he was wrong to add 23, 29, and 37 to his prime numbers list. Soon others discovered his errors, including French mathematician Pierre de Fermat (1601–1665) in 1640, and Swiss mathematician Leonhard Euler (1707–1783) in 1738.
The hunt for primes continued. The name “Mersenne” actually came from French priest, Father Marin Mersenne (1588–1648) who in 1644 referred to such numbers in the preface to his book Cogitata Physica-Mathematica. He believed that these special primes were: p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257. But like earlier attempts at determining prime numbers, many of Mersenne’s numbers were in error. It took three centuries more to check Mersenne’s range of numbers, and by 1947, the correct list of Mersenne primes were: p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 and 127. Interestingly enough, even though Mersenne incorrectly stated certain numbers belonged to this group—he probably didn’t verify all the numbers on his list—his name is still attached to the numbers.