What Is the World Made Of?Introduction |
How can the emission and absorption of light by atoms be explained? |
In 1911 Niels Bohr (1885-1962), a Dane who recently had received his Ph.D. from the University of Copenhagen, joined Rutherford at Cambridge University. He quickly began work on the Rutherford model. He published his results in 1913, basing them on three postulates.
- Electrons only move in certain allowed orbits at discrete radii and with specific energies. That is, their radii and energies are “quantized.” When in these orbits their radii and energies are constant. The atoms do not emit or absorb radiation.
- Electrons gain or lose energy when they jump from one allowed orbit to another. Then they emit or absorb light with a frequency given by hf=E2 - E1 where E2 and E1 are the energies of the electrons in the allowed orbits. The constant h is called Planck’s constant, 6.6 x 10-34 J/Hz (joules per hertz).
- The correspondence principle. When the electron is very far away from the nucleus classical physics must give the same answer as the new quantum physics.
He later changed the third postulate from the correspondence principle to requiring that the angular momentum of the electron be quantized, that is proportional to an integer called the quantum number. The results didn’t change, but the derivation of them was more straightforward. This method is presented in almost every textbook.
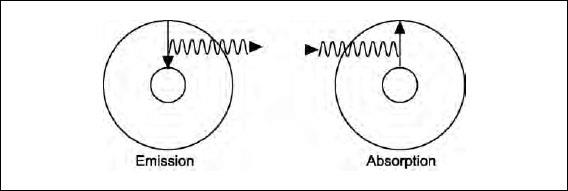
The two drawings below illustrate the emission of light when the electron goes from a higher-energy to a lower-energy orbit and the absorption of light when the electron’s energy is increased.
In 1885 Johann Balmer had found a formula that accurately calculated the wavelengths of the visible hydrogen spectrum. It was purely empirical—that is, there was no physics-based explanation of it. In 1888 Janne Rydberg generalized Balmer’s results to allow calculation of hydrogen emission in the ultraviolet and infrared. Bohr was able to explain Balmer’s and Rydberg’s formulae using the results of his postulates. The equation for the wavelength of the emitted radiation is 1/ λ = R(1/m2 - 1/n2). The numbers m and n are the quantum numbers of the two energy levels. For example, the red line would have m = 2, n = 3. The constant R is 0.01097 nm-1, making the wavelength of the red line 1/(0.01097 (¼ - 1/9) nm-1) = 656.3 nm, in excellent agreement with the experiment. Thus Bohr’s model is a major advance in understanding the structure of the atom.