Millions of psychology majors grit their teeth and roll their eyes at the very thought of statistics. Nonetheless, statistics are a fundamental part of psychological research. Statistics provide a mathematical technique to measure the relationships between two or more variables (traits of interest such as intelligence, aggression, or severity of depression). Statistics can show how these variables relate. It can show the strength of their relationship and the probability that the relationships found in a given study are likely to be true findings, rather than a statistical fluke, i.e., due to chance. The most common statistics are measures of central tendencies, specifically: the mean, median, and the mode; measures of group differences such as the t-test, ANOVA, and MANOVA; and measures of covariation, such as correlation, factor analyses, and regression analyses. Measures of covariation assess the degree to which two or more variables change in relation to each other. For example, height and weight covary (or are correlated) while age and ethnicity do not. In general tall people weigh more than shorter people while ethnicity does not change with age.
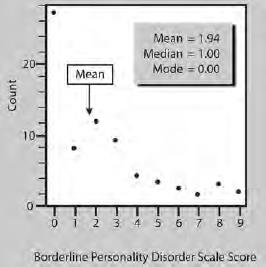
This is a graph showing how 69 people scored on a test measuring traits of a personality disorder. The vertical axis represents the count, or the number of people who attained each score. The horizontal axis represents the scale score. In this graph, the vast majority of the subjects scored on the low end of the scale while a few people had much higher scores. When the distribution of scores is concentrated toward one end of the scale, we say there is a skewed distribution. In a normal distribution the majority of scores are in the middle with a few scores moving out toward the far ends of either side. When the distribution is skewed like this, the mean, median, and mode separate from each other.

