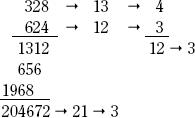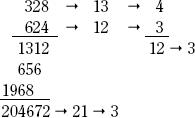The method of “casting out nines” is based on the excess of nines in digits of whole numbers (the remainder when a sum of digits is divided by 9). Illustrating this process in the multiplication example below, the method begins by adding the digits in both the multiplicand (one of the terms that is being multiplied) and the multiplier (the other term being multiplied). In the example below, this operation leads to the results of “13” and “12,” respectively. If these results are greater than 9 (>9), then the operation is repeated until the resulting figures are less than 9 (<9). in="" the="" example="" below,="" the="" repeated="" calculation="" gives="" the="" results="" as="" “4”="" and="" “3,”="" respectively.="" multiply="" the="" resulting="" “excess”="" from="" the="" multiplicand="" by="" the="" excess="" from="" the="" multiplier="" (4="" 3="" 3="" below).="" add="" the="" digits="" of="" the="" result="" to="" eventually="" yield="" a="" number="" equal="" to="" or="" less="" than="" 9="" (="9)." repeat="" the="" process="" of="" casting="" out="" nines="" in="" the="" multiplication="" product="" (the="" result="" of="" the="" multiplication="" process).="" the="" result="" must="" equal="" the="" result="" of="" the="" previous="" set="" of="" transactions,="" in="" this="" case="" “3.”="" if="" the="" two="" figures="" disagree,="" then="" the="" original="" multiplication="" procedure="" was="" done="" incorrectly.="" “casting="" out="" nines”="" can="" also="" be="" applied="" to="" check="" the="" accuracy="" of="" the="" results="" of="">