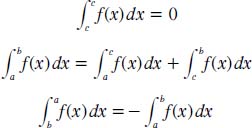There are several useful properties of the definite integral. Theorem one is based on the idea that if f(x) and g(x) are defined and continuous on [a, b], except perhaps at a finite number of points, then the following applies in which alpha is a constant:

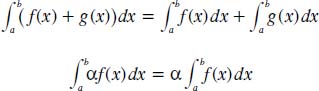
Theorem two is based on the idea that if f(x) is defined and continuous on [a, b], except at a finite number of points, then the following applies for any arbitrary numbers a and b, and any c ∈ [a, b]: