In actuality, the area shown on page 233 is actually determined using limits. In the function f(x), as n gets larger, the numbers determined by left (n) and right (n) will get closer and closer to the area Ω. This is seen as the following notation:

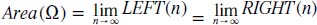
Thus, in the calculus terms, the area of the above graphic region is called the definite integral (also said as “the integral”) of f(x) from a to b, and is denoted by the following notation:

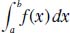
The variable x can be replaced with any other variable. In other words, if the limits of integration (a and b) are specified, it is called a definite integral, and it can be interpreted as an area or a generalization of an area.